Exercice 4 - Galaxy Clusters as Gravitational Lenses¶
In this practical work, we will make use of deep images of the massive galaxy cluster Abell 370 (A370 in the following). You have been given three frames obtained with the ESO VLT through three filters. They consist of numerous short exposures that have already been reduced as explained in Chapter 1 of this booklet. The reduced exposures have also been combined into one single frame that allow to see very faint objects.
Among the numerous objects in the images are distant galaxies, nearby galactic stars and a massive galaxy cluster. We will use the images in order to estimate the mass of the galaxy cluster and study the color distribution of galaxies in the cluster.
4.1 - The Cluster as a Gravitational Lens¶
Following Einstein’s equivalence principle between gravity and
inertial forces, all bodies even with no mass, are under the influence
of gravitation. As a direct consequence, a photon can be attracted by
a massive body such as a galaxy or a galaxy cluster. As an optical
lens does, a mass modifies the path followed by photons and therefore
acts as a gravitational lens. The angle by which the light rays
are bended by an object with a mass 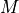 can be calculated in the
context of Einstein’s theory of general relativity, as:
can be calculated in the
context of Einstein’s theory of general relativity, as:
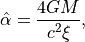
where 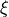 is the impact parameter of the light ray (see
Fig. 1. Compute the value of
is the impact parameter of the light ray (see
Fig. 1. Compute the value of 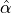 for the mass of
the sun. The impact parameter can be approximated by the radius of the
sun.
for the mass of
the sun. The impact parameter can be approximated by the radius of the
sun.
Fig. 1 gives a schematic description of the phenomenon
of gravitational lensing, where a source 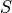 is lensed by a massive
object in the lens plane (labeled
is lensed by a massive
object in the lens plane (labeled 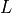 ). The source is not seen at its
real angular position
). The source is not seen at its
real angular position 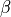 by the observer
by the observer 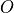 , but is displaced by
an angle
, but is displaced by
an angle 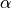 that depends on the true deflection angle
that depends on the true deflection angle
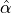 .
.
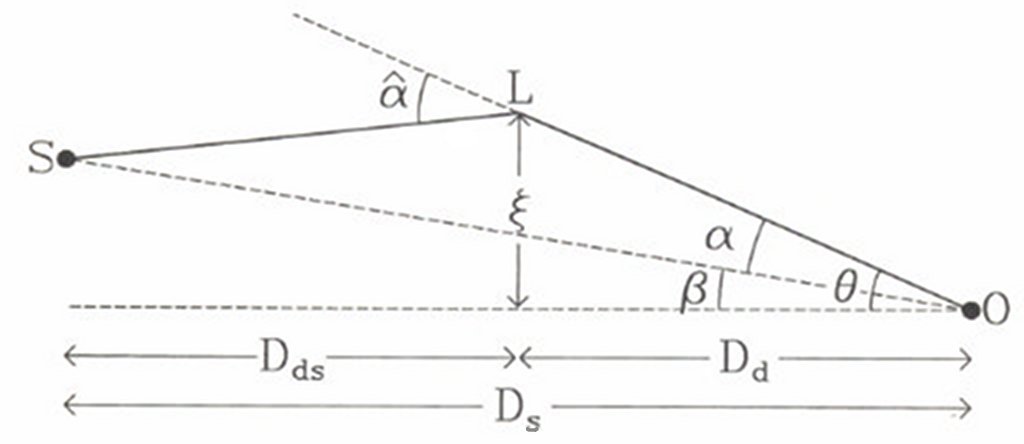
Fig.1 : Schematic view of the gravitational lensing effect. The
observer “O” sees the image “L” of the source “S” at a position
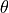 on the plane of the sky. The source
on the plane of the sky. The source 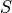 is never
observable. The lensing galaxy is also called the deflector, hence
the indices used to label the different distances.¶
is never
observable. The lensing galaxy is also called the deflector, hence
the indices used to label the different distances.¶
If we assume that the distances between the different
objects are known show that, when the source, the lens and the
observer are almost perfectly aligned (i.e., 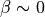 ):
):
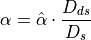
When the source is perfectly aligned with the
observer and then lens (i.e., 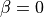 ), it is imaged into a ring
called an Einstein ring. Using Fig. 1 and simple
geometrical considerations, show that the Einstein radius is:
), it is imaged into a ring
called an Einstein ring. Using Fig. 1 and simple
geometrical considerations, show that the Einstein radius is:
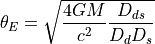
All the above is true only when the distances involved in the
calculations are angular diameter distances. As the reference
used to measure distances changes with redshift (i.e., the ruler you
are using to measure distances is changing with the redshift), angular
diameter distances are given under the form of an integral. The
distance between two objects at redshifts 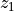 and
and 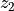 (
(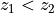 )
is given by:
)
is given by:
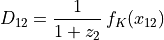
with
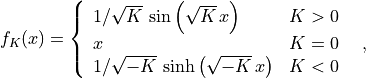
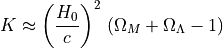
and
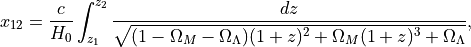
where 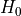 is the Hubble parameter,
is the Hubble parameter, 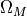 is the density of
matter of the universe, normalised to its total density and
is the density of
matter of the universe, normalised to its total density and
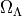 is the density associated to the vacuum. From the
most recent studies using distant supernovae, the current values of
these parameters are
is the density associated to the vacuum. From the
most recent studies using distant supernovae, the current values of
these parameters are 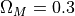 and
and 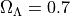 . The value
of
. The value
of 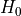 is still poorly known. The currently more accepted (but probably
biased) value is
is still poorly known. The currently more accepted (but probably
biased) value is 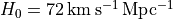 .
.
As the integral above can not be calculated explicitly, integrate it numerically to compute the distance between us (
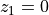 ) and an object at redshift
) and an object at redshift 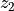 .
You could code your own elementary integration, or use one of
.
You could code your own elementary integration, or use one of scipy.integrate’s numerous possibilities.Make a graph showing the distance as a function of redshift. Also plot the Hubble relation for comparison. Of course this relation is valid only at very low redshifts. At
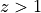 it would
even imply that galaxies have velocities larger than the speed of
light. The Hubble law, in its original form does not take relativistic
corrections into account.
it would
even imply that galaxies have velocities larger than the speed of
light. The Hubble law, in its original form does not take relativistic
corrections into account.Using the three VLT images of A370, make a color image, as was done for NGC 613. You can use for instance
stiffor the log scale option ofds9. Later you can fine-tune the color scale using the color editor ingimpin order to emphasize the color contrast between the different objects in the field of view.You notice immediately an overdensity of galaxies that seem to have the same color. These galaxies belong to the A370. Give a plausible reason for them being of the same color.
An arc-like structure is seen close to the center of the cluster. This arc is not physically in the cluster but corresponds to a gravitationally lensed galaxy in the background of the cluster. The redshift of the arc is
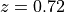 while the redshift of the cluster is
while the redshift of the cluster is
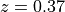 . Compute the angular diameter distances to the cluster and to
the arc as well as the distance between the cluster and the arc.
. Compute the angular diameter distances to the cluster and to
the arc as well as the distance between the cluster and the arc.The pixel scale in the image is 0.2 arcseconds. Considering the arc as a part of an Einstein ring, measure the angular Einstein radius of the cluster. Give an estimate of the mass of the cluster.
If the lensing mass is considered as an isothermal sphere, its Einstein radius can be expressed as a function of the velocity dispersion following:
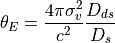
Give an estimate of the velocity dispersion of the lens. How does this compare with the velocity dispersion measured in the second chapter for the same object ? If you find a difference, try to explain it.
